背景

最近阅读一些零次学习的相关论文，枢纽点问题hubess是经常出现的一个概念，对于这个概念的理解较少，只知道是会影响到零次学习的模型性能，也是 KNN(k nearest neighbors)会出现的一个现象，后来阅读了论文 Hubs in Space: Popular Nearest Neighbors in High-Dimensional Data 有了更深一步的了解。

论文地址

简述

基本概念

在介绍本文内容之前需要了解一些相关概念。

偏态分布

偏态分布(skew distribution)是与正态分布相对，分布曲线左右不对称的数据次数分布，是连续随机变量概率分布的一种。可以通过峰度和偏度的计算，衡量偏态的程度。可分为正偏态和负偏态，前者曲线右侧偏长，带有一个较长的尾巴，左侧则偏短，后者曲线在左侧有一个较长的尾巴，右侧偏短。 偏离程度可以用一个偏离系数表示，偏离稀疏大于0则表示正偏态，小于0则为负偏态，等于0则是正态分布。

$\chi ^{2}$分布

卡方分布（chi-square distribution）是概率论与统计学中常用的一种概率分布。$k$ 个独立的标准正态分布变量的平方和服从自由度为$k$的卡方分布. 数学定义 若随机变量$ Z_1, \cdots, Z_k$是互相独立，且符合标准正态分布的随机变量，则他们的平方和 \(X=\sum_{i=1}^{k}{Z_{i}}^{2}\) 服从自由度为 $k$ 的卡方分布，记作 $X \sim \chi^{2}(k)$.

卡方分布的概率密度函数为：

\[f_k(x)=\frac{\frac{1}{2}^{\frac{k}{2}}}{\Gamma({\frac{k}{2}})}x^{\frac{k}{2}-1}e^{-\frac{x}{2}}\]

这里的 $\Gamma(\cdot)$是伽马函数，是阶乘函数在实数与复数上的扩展，如果 $n$ 为正整数，则 $\Gamma(n)=(n-1)!$, 对于实数部分为正数的复数 $z$, 伽马函数定义为： \(\Gamma(z)=\int_{0}^{\infty} \frac{t^{z-1}}{e^{t}}\mathbf{d}t\)

维度灾难

维度灾难是指随着维度的增加，数据的分布会出现一些异于低维空间的现象，这些现象给当前各种各样的机器学习模型带来了不少的挑战与困难。比较常见的维度灾难现象是数据稀疏性，距离浓缩(distance concentration)。数据稀疏性比较好理解，对于100个数据点，如果放在一维空间内的10个单位距离内，那么每个单位距离内很可能会包含数据点，但是如果对于二维空间内，就有一个100个单位，每个单位包含数据点的可能性就比较低，对于更高维空间，则每个单位内包含的数据点的概率就会极低。距离浓缩的意义为高维空间内的大部分点都远离其中心，距离的远近实际上已经变得很难区分，数学形式表示为：

\[\lim _{d \rightarrow {\infty}} \frac{dist_{max}-dist_{min}}{dist_{min}} \approx 0\]

在这种情形下，低维空间中常用的欧式距离等度量方式已经不太可行，对于像KNN这样的机器学习模型有着较大的影响。

本文探索研究了一种新的维度灾难现象即枢纽点问题(hubness)。具体而言就是：随着数据的维度的增加，会出现一些顺枢纽点，这些枢纽点相比于其它数据点会频繁作为数据点的K个最近的邻居出现，打一个比方就是，在一个类似于数据点的人类社会体系中，一些人的人脉关系比较强，和其他大多数人都有比较近的交往。

数学形式化表示：假设 $\mathcal{D} \subset \mathbb{R}^{d} $ 是一个 $d$ 维的数据点集合，用 $N_{k}(\mathbf{x})$ 表示数据点 $\mathbf{x}$ 在一定的距离计算规则下作为其他数据点 $k$ 近邻出现的次数。

在一般的条件情形下，随着数据维度的升高， $N_{k}$ 的分布会更加趋向于正偏态分布。

关于枢纽点问题需要说明两点：

• 枢纽点问题和距离浓缩两种现象是相关的，但是不同的两个现象，距离浓缩是说随着维度的升高，数据点到原点(或者其它参考点)的距离，乃至任意两个点的距离都会趋近于一定的数值，而枢纽点问题的根源来自于这些距离的趋近速度是不相同的，好比一个班的同学都是想在期末考试中考满分，但是有的同学往这个目标靠近的比较快，而有的同学则进步的比较慢，渐渐地，同学之间也就拉开了差距。

• 枢纽点问题是高维数据空间的一个本质内在特征，而不是由于某一个数据集的特性或者人工干预导致的。

枢纽点问题

合成数据集上的枢纽点问题

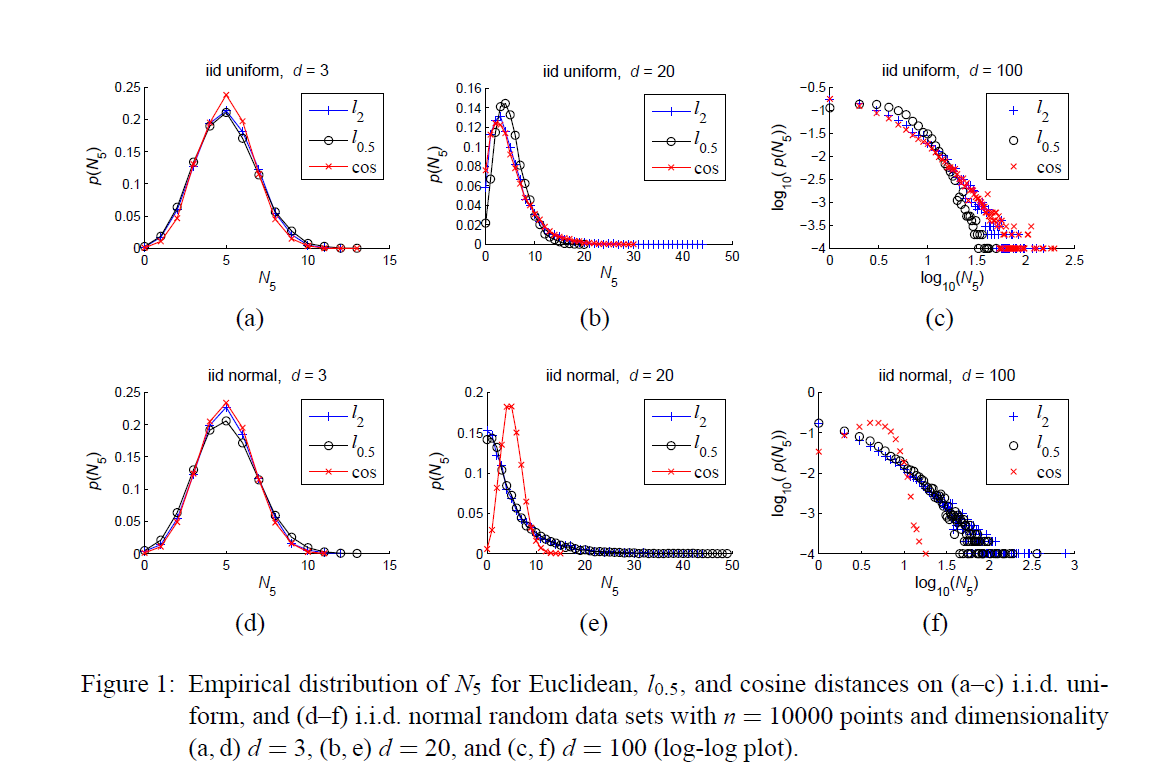
前面已经叙述了 $N_{k}$ 的含义，现在我们通过一些实验观察人工合成的数据集 $N_{k}$ 的分布情况。作者考察的是10000个范围0-1的均匀分布数据点，每个数据点的维度为 $d$ ，每个维度之间独立同分布。此外选择三种距离度量方式 (1) Euclidean($l_2$). (2) Fractional($l_{0.5}$) (3) Cosine

下图 a、b、c 均匀分布得到的不同维度数据点的 $N_5$ 分布，d、e、f是正态分布下得到不同维度数据点的 $N_5$分布。可以看到随着维度的升高， $N_5$ 分布逐渐呈现正偏态：曲线右半部分有一个长长的尾巴。此外作者还考察了其它分布以及 $k$ 值($k \ll n$)下的情形, $n$ 为数据点个数，结果均为随着维度升高，分布出现正偏态，导致了枢纽点的产生。不过在正态分布用Cosine度量的情况下出现了反常的情况，而这在实际情况中是很少涉及的，在论文的5.2小节详细介绍了高维中出现枢纽点的充分条件。

真实数据集上的枢纽点问题

论文主要考察了50个来自于著名源网站的数据集，这些数据集相关信息列在表1中。

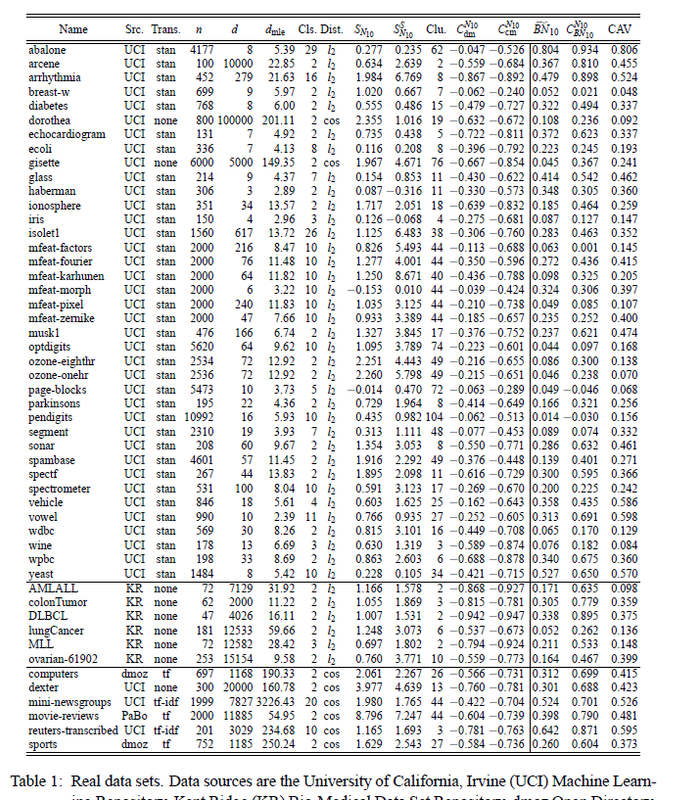
表格的第四列表示的是使用到的数据点数，第五列是数据的维度，第七列是数据的种类数目，第八列是使用到的距离度量方式。

为了描述 $N_k$ 分布的不对称程度，文章使用了变量 $N_k$ 的三阶矩去描述。

\[S_{N_{k}}=\frac{\mathbf{E}(N_{k}- \mu_{N_{k}})^{3}}{\sigma_{N_{k}^{3}}}\]

这里的 $\mu_{N_{k}}$ 和 $\sigma_{N_{k}}$ 分别为 $N_{k}$ 的均值和标准差， 表格中的第九列表示的就是 $S_{N_{10}}$。可以看到数据集中该值基本都大于0，这表明数据集的 $N_{k}$ 分布不对称，且呈正偏态分布，值越大，不对称程度越明显，数据的枢纽点情况越严重。此外还计算了维度 $d$ 和 $S_{N_{k}}$ 之间的皮尔曼相关系数(Spearman correlaiton), 结果表明相关性很强。

另一方面在真实数据集中的枢纽点问题并没有像合成数据集那样对数据的维度那么敏感，对于此文章也给出了解释：真实数据集中的数据本征维度或者说有效维度并不是等于数据的维数，因为不数据的不同维之间往往存在某种程度上的关联，因此本征维度往往小于数据维度 $d$。

枢纽点问题的根源

前面我们通过实验已经观察到不管是在真实数据集上还是合成数据集上随着维度升高会出现枢纽点， $N_k$ 分布会呈现严重的不对称情况。那么这一节介绍枢纽点问题出现的原因和背后的机制。

首先呢我们需要了解的是一个点能否成为枢纽点与它距离数据集的中心位置远近程度有很大关系，对于一个单峰分布的数据集而言，越靠近数据集的中心，则越可能成为高维空间中的枢纽点。多峰分布则是单峰分布的混合，这样的分布情况，枢纽点则靠近混合分布的一个单峰分布的中心处(均值)。

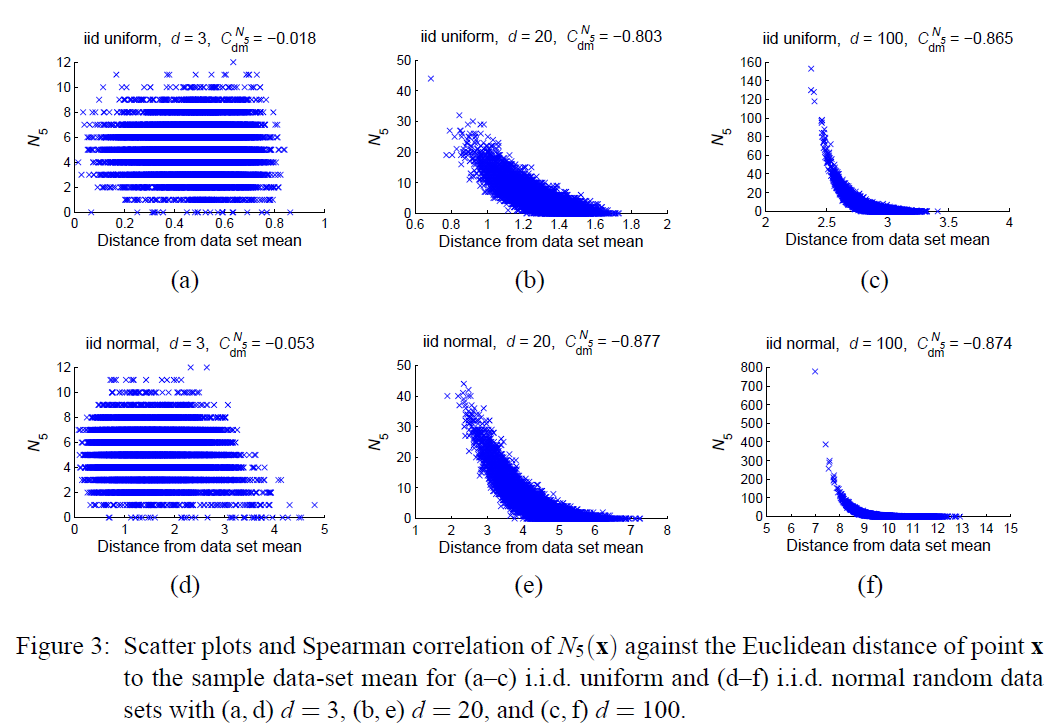
前面已经介绍过距离浓缩这个问题，随着维度的升高，数据点之间的差别(方差) 和数据到数据集中心点的距离的比值会趋近极小的值，好比于一个三维球空间，数据点大都分布在最外面薄薄的一层，高维空间可以看做是一个特殊的球体。另一个方面，对于有限的维度来说，数据分布的标准差也是不能忽略的， 因此在高维空间中存在一定数量的比较靠近数据集中心的点。

关于上面结论更为详细的解释：

根据定义有到数据中心点的欧氏距离实际上是自由度为 $d$ 的卡方分布， 而且根据相关研究表明，随着维度的升高，数据到数据中心点距离分布的方差呈现趋近某个常数的趋势(一些度量下趋近于0)，而距离的均值则与 $\sqrt{d}$ 成正相关。那么对于有限的 $d$ 来说，存在的方差总会使得有些点比其它点更靠近中心点。

下图是不同维度下到正态分布均值点的距离分布曲线：

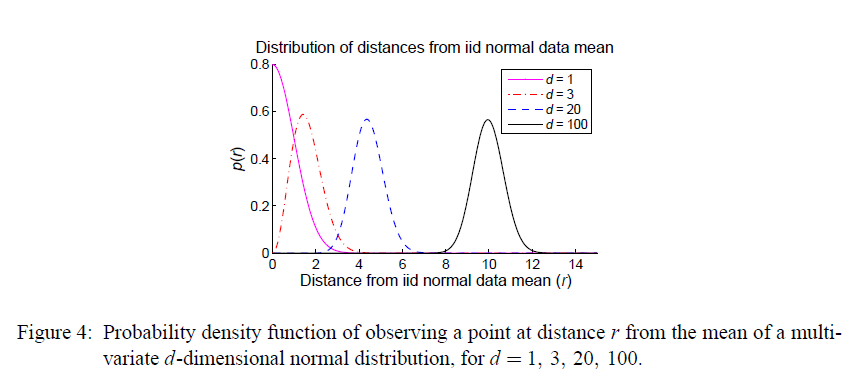
接下来我们需要了解的一个事实是：靠近数据集均值的数据点会在高维空间中成为枢纽点。 为了理解为什么会这样，文章举了个例子，在独立正态分布条件下，取了两个点 $a_d, b_d$,后者距离原点(或者其它任意参考点，结论都是成立的)指定的距离， 前者则是缩短了两倍标准差的距离(距离相同的参考点)，那么随着维度的不断变化，会分别有两个系列的点集合 $a_{d}s, b_{d}s$, 实际上这些点到其它数据集的点的距离的分布是偏差为 $\lambda$（这里$\lambda$等于 $a_d$ 或者 $b_d$ 到原点的距离），自由度为 $d$ 的卡方分布。而且两个分布(分别对应 $a_d$ 和 $b_d$ )随着维度的升高逐渐远离即：随着维度的升高，距离原点近的点 $b_d$ 到其它数据点的均值与距离原点更远的点 $a_d$ 到其它数据点的均值之间的差别会变大。如下图所示

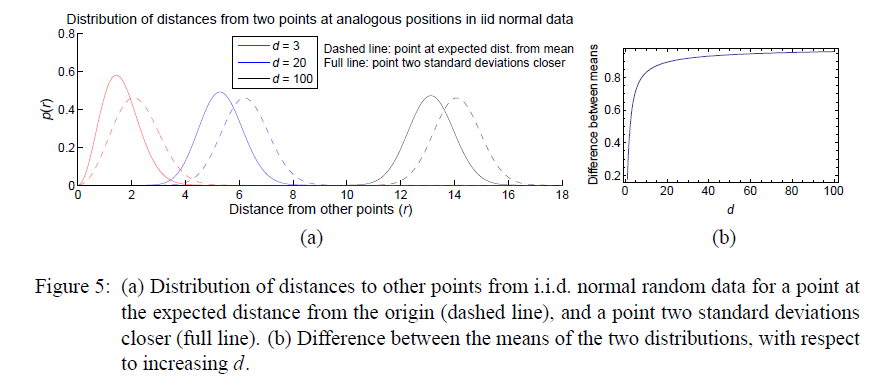
那么现在我们知道了越是靠近数据集均值位置的数据点总体上越比较靠近其它任何的点，而且这种差别会因为维度的升高而被放大，好像班级的学习努力成绩好的同学与不努力成绩差的同学，会随着时间的增长，成绩差别会越来越大，虽然二者都会进步但是学习吸收知识的速度不一样。到这呢也就解释了为什么高维空间中靠近数据集中心的点越容易成为其它点的最近邻点。

同时作者用数学的形式描述了这一定理。在独立同正态分布条件下， 两个点到数据集均值的距离分别表示为 \(\lambda_{d,1}=\mu_{\chi(d)}+c_{1}+\sigma_{\chi(d)}, \lambda_{d,2}=\mu_{\chi(d)}+c_{2}+\sigma_{\chi(d)}\) $\mu_{\chi(d)}, \sigma_{\chi(d)}$ 分别是数据点到中心点(数据集均值)的距离的分布的均值和标准差， 前面那个例子实际上就是 $c_1=-2, c_2=0$, 实际上对于任意的 $c_1, c_2$ 上面的例子都是成立的。为了数学表述，作者用 $\mu_{\chi(d, \lambda_{d,i})}$表示距离中心点为 $\lambda_{d,i}$的点到其它点距离的分布(前面例子中已经提到了，该分布是一个卡方分布，其偏差就等于该点到原点的距离)的均值，$i \in {1, 2}$, 用 \(\Delta \mu_{d}(\lambda_{d,1}, \lambda_{d,2})=\|\mu_{\chi(d, \lambda_{d,2})}- \mu_{\chi(d, \lambda_{d, 1})}\|\) 表示两个点的分布均值的差值， $d$ 表示数据的维度，可得数学定理如下：

对任意大于0的正整数 $d_0$，总有任意的正整数 $d$, $d > d_0$, 使得：

\[\Delta_{\mu_{d}}(\lambda_{d,1}, \lambda_{d, 2}) > 0\]

且有

\[\Delta_{\mu_{d+2}}(\lambda_{d+2, 1}, \lambda_{d+2, 2}) > \Delta_{\mu_{d}}(\lambda_{d,1}, \lambda_{d, 2})\]

讲真的，我不太清楚这里为什么有个2，而不是其它数，作者也没有相关说明，疑惑？？？

进一步探索真实数据集上的枢纽点

作者关于真实数据集主要研究了两个问题：

• 不同于人工设定的数据集，真实数据集的属性之间有关联，也就是说不是独立同分布关系
• 真实数据集的分布不是单峰分布，往往是多峰分布，这些数据可以根据聚类方法分为若干类，每一类各有一个中心点。

关于数据集的属性之间存在一定的关联性，得出了一个结论：数据集的枢纽点现象与数据集的本征维度相关程度要比原始维度强，本征维度中的每个维度近似是独立同分布的关系，这也解释了真实数据集枢纽点问题随着维度上升影响不大的问题。

关于多峰分布，得出的结论是：数据点的 $N_k$ 变量分布与该点到相应的聚类中心点的距离皮尔曼相关系数比到数据集总体中心点距离的皮尔曼相关系数更大。